Rovnostranný trojuholník je trojuholník so všetkými tromi stranami rovnakej dĺžky. Povrchová plocha dvojrozmerného mnohouholníka, napríklad trojuholníka, je celková plocha, ktorú tvoria strany mnohouholníka. Tri uhly rovnostranného trojuholníka sú rovnako rovnaké v euklidovskej geometrii. Keďže celková miera uhlov euklidovského trojuholníka je 180 stupňov, znamená to, že všetky uhly rovnostranného trojuholníka merajú 60 stupňov. Oblasť rovnostranného trojuholníka sa môže vypočítať, ak je známa dĺžka jednej jeho strany.

Určite plochu trojuholníka, keď je známa základňa a výška. Zoberte dva rovnaké trojuholníky so základňou s a výškou h. S týmito dvoma trojuholníkmi môžeme vždy vytvoriť rovnobežník báz a výšky h. Pretože plocha rovnobežníka je s x h, plocha A trojuholníka je preto ½ s x h.

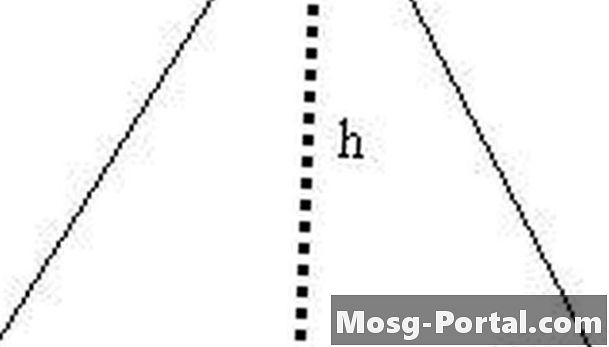
Rovnostranný trojuholník vytvorte do dvoch pravouhlých trojuholníkov so čiarou h. Prepona jedného z týchto pravouhlých trojuholníkov má dĺžku s, jedna noha má dĺžku ha druhá noha má dĺžku s / 2.
Vyjadrte h v zmysle s. Použitím pravouhlého trojuholníka vytvoreného v kroku 2 vieme, že s ^ 2 = (s / 2) ^ 2 + h ^ 2 podľa Pythagorovho vzorca. Preto h ^ 2 = s ^ 2 - (s / 2) ^ 2 = s ^ 2 - s ^ 2/4 = 3s ^ 2/4 a teraz máme h = (3 ^ 1/2) s / 2.
Nahraďte hodnotu h získanú v kroku 3 do vzorca pre oblasť trojuholníkov získanú v kroku 1. Pretože A = ½ sxh a h = (3 ^ 1/2) s / 2, máme teraz A = ½ s (3 ^) 1/2) s / 2 = (3 ^ 1/2) (s ^ 2) / 4.
Použite vzorec pre oblasť rovnostranného trojuholníka získaného v kroku 4 a nájdite plochu rovnostranného trojuholníka so stranami dĺžky 2. A = (3 ^ 1/2) (s ^ 2) / 4 = (3 ^ 1/2 ) (2 ^ 2) / 4 = (3 ^ 1/2).