Elipsa môže byť definovaná v rovinnej geometrii ako množina bodov tak, že súčet ich vzdialeností k dvom bodom (ohniskám) je konštantný. Výsledná hodnota môže byť tiež opísaná nematematicky ako oválny alebo „sploštený kruh“. Elipsy majú mnoho aplikácií vo fyzike a sú obzvlášť užitočné pri popisovaní planétových dráh. Excentricita je jednou z charakteristík elipsy a je mierou kruhovej elipsy.
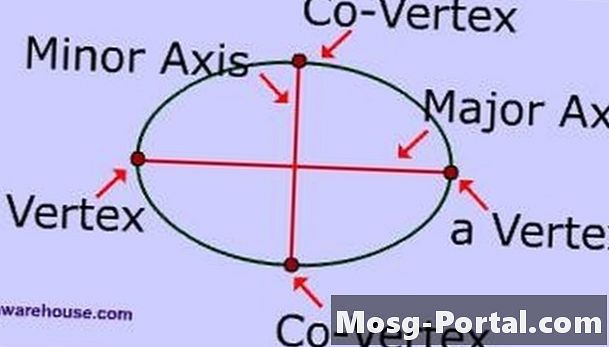
Preskúmajte časti elipsy. Hlavná os je najdlhší úsečka, ktorá pretína stred elipsy a má svoje koncové body na elipse. Vedľajšia os je najkratšou čiarou, ktorá pretína stred elipsy a má svoje koncové body na elipse. Hlavná poloos je polovica hlavnej osi a vedľajšia poloos je polovica hlavnej osi.
Skontrolujte vzorec pre elipsu. Existuje mnoho rôznych spôsobov matematického popisu elipsy, ale najužitočnejší spôsob výpočtu jej excentricity je elipsa: x ^ 2 / a ^ 2 + y ^ 2 / b ^ 2 = 1. Konštanty a a b sú špecifické pre konkrétnu elipsu a premenné sú súradnice bodov x a y bodov, ktoré ležia na elipse. Táto rovnica popisuje elipsu so stredom na začiatku a hlavnými a vedľajšími osami, ktoré ležia na počiatkoch xay.
Identifikujte dĺžky poloosí. V rovnici x ^ 2 / a ^ 2 + y ^ 2 / b ^ 2 = 1 sú dĺžky poloosí dané a a b. Väčšia hodnota predstavuje hlavnú poloosu a menšia hodnota predstavuje vedľajšiu poloosu.
Vypočítajte polohy ohnísk. Ohniská sú umiestnené na hlavnej osi, jedna na každej strane stredu. Pretože osi elipsy ležia na pôvodných líniách, jedna súradnica bude 0 pre obe ohniská. Druhá súradnica bude (a ^ 2 - b ^ 2) ^ (1/2) pre jednu ohnisku a - (a ^ 2 - b ^ 2) ^ (1/2) pre ďalšie ohniská, kde a> b.
Vypočítajte excentricitu elipsy ako pomer vzdialenosti zaostrenia od stredu k dĺžke poloosy. Excentricita e je preto (a ^ 2 - b ^ 2) ^ (1/2) / a. Všimnite si, že 0 <= e <1 pre všetky elipsy. Excentricita 0 znamená, že elipsa je kruh a dlhá, tenká elipsa má excentricitu, ktorá sa blíži 1.