Obsah
V geometrii je osemuholník mnohouholník s ôsmimi stranami. Pravidelný osemuholník má osem rovnakých strán a rovnaké uhly. Pravidelný osemuholník sa bežne rozpoznáva podľa značiek. Osemsten je osemstranný mnohosten. Pravidelný osemsten má osem trojuholníkov s okrajmi rovnakej dĺžky. Na ich základniach sa skutočne stretávajú dve štvorcové pyramídy.
Octagon Area Formula
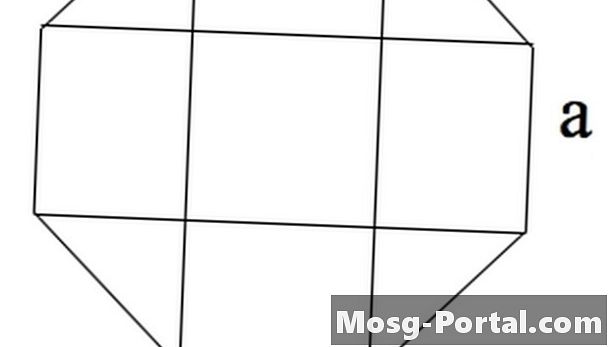
Vzorec pre oblasť pravidelného osemuholníka so stranami dĺžky „a“ je 2 (1 + sqrt (2)) a ^ 2, kde „sqrt“ označuje druhú odmocninu.
derivácie
Osemuholník je viditeľný ako 4 obdĺžniky, jeden štvorec v strede a štyri rovnoramenné trojuholníky v rohoch.
Štvorec má plochu a ^ 2.
Trojuholníky majú strany a, a / sqrt (2) a / sqrt (2), podľa Pythagorovej vety. Preto každá z nich má plochu ^ 2/4.
Obdĺžniky majú plochu a * a / sqrt (2).
Súčet týchto 9 oblastí je 2a ^ 2 (1 + sqrt (2)).
Octahedron Volume Formula
Vzorec pre objem obyčajného osemstena strán "a" je ^ 3 * sqrt (2) / 3.
derivácie
Plocha štvorstrannej pyramídy je plocha základne * výška / 3. Plocha pravidelného osemuholníka je preto 2 * základňa * výška / 3.
Base = a ^ 2 triviálne.
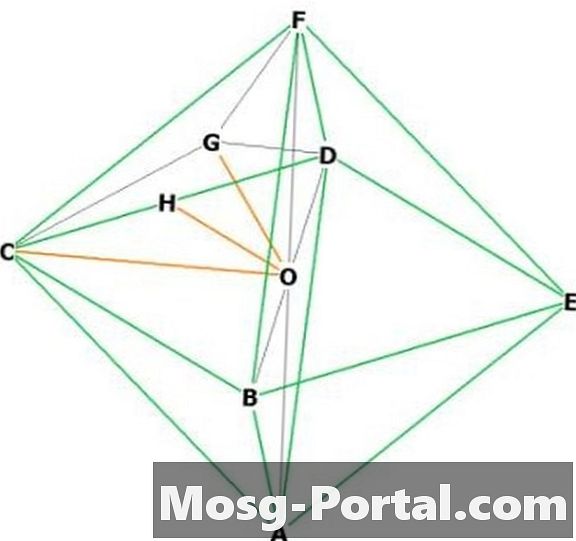
Vyberte dva susedné vrcholy, povedzte „F“ a „C.“ "O" je v strede. FOC je rovnoramenný pravouhlý trojuholník so základňou „a“, takže OC a OF majú dĺžku a / sqrt (2) podľa Pythagorovej vety. Výška = a / sqrt (2).
Objem normálneho oktaedronu je 2 * (a ^ 2) * a / sqrt (2) / 3 = a ^ 3 * sqrt (2) / 3.
Plocha povrchu
Pravidelný povrch osemstien je plocha rovnostranného trojuholníka s bočnými „a“ časmi 8 tvárí.
Ak chcete použiť Pythagorovu vetu, presuňte čiaru z vrcholu na základňu. Takto sa vytvoria dva pravé trojuholníky s preponou dĺžky „a“ a dĺžky jednej strany „a / 2“. Preto tretia strana musí byť sqrt = sqrt (3) a / 2. Takže oblasť rovnostranného trojuholníka je výška * základňa / 2 = sqrt (3) a / 2 * a / 2 = sqrt (3) a ^ 2/4.
Pri ôsmich stranách je plocha normálneho osemstena 2 * sqrt (3) * a ^ 2.