Tangens je jednou z troch základných trigonometrických funkcií, ďalšie dve sú sine a cosine. Tieto funkcie sú nevyhnutné pre štúdium trojuholníkov a spájajú uhly trojuholníka s jeho stranami. Najjednoduchšia definícia dotyčnice využíva pomery strán pravouhlého trojuholníka a moderné metódy túto funkciu vyjadrujú ako súčet nekonečnej série. Tangenty sa môžu vypočítať priamo, keď sú známe dĺžky strán pravého trojuholníka a dajú sa odvodiť aj z iných trigonometrických funkcií.
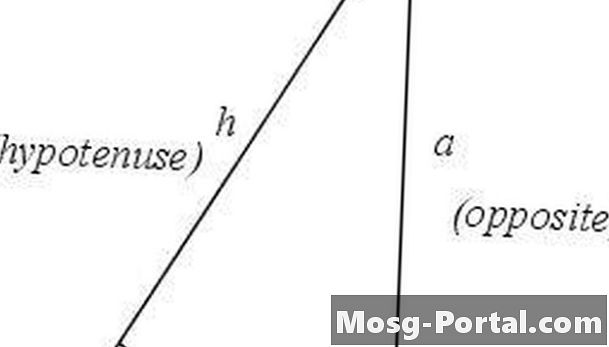
Identifikujte a označte časti pravouhlého trojuholníka. Pravý uhol bude na vrchole C a na protiľahlej strane bude prepona h. Uhol 9 bude vo vrchole A a zostávajúci vrchol bude B. Strana susediaca s uhlom 9 bude strana b a strana opačná uhol 9 bude strana a. Obe strany trojuholníka, ktoré nie sú preponou, sa nazývajú nohy trojuholníka.
Definujte dotyčnicu. Dotyčnica uhla je definovaná ako pomer dĺžky strany protiľahlej k uhlu k dĺžke strany priľahlej k tomuto uhlu. V prípade trojuholníka v kroku 1, tan 9 = a / b.
Určite dotyčnicu pre jednoduchý pravouhlý trojuholník. Napríklad, nohy rovnoramenného pravouhlého trojuholníka sú rovnaké, takže a / b = tan θ = 1. Uhly sú rovnako rovnaké 9 = 45 stupňov. Preto opálenie 45 stupňov = 1.
Odvodte dotyčnicu od ostatných trigonometrických funkcií. Pretože sínus 9 = a / h a kosínus 9 = b / h, potom sínus 9 / kosínus 9 = (a / h) / (b / h) = a / b = tan 9. Preto tan 9 = sínus 9 / kosínus 9.
Vypočítajte dotyčnicu pre akýkoľvek uhol a požadovanú presnosť:
sin x = x - x ^ 3/3! + x ^ 5/5! - x ^ 7/7! + ... cosine x = 1 - x ^ 2/2! + x ^ 4/4! - x ^ 6/6! + ... Takže tan x = (x - x ^ 3/3! + X ^ 5/5! - x ^ 7/7! + ...) / (1 - x ^ 2/2! + X ^ 4 / 4! - x ^ 6/6! + ...)