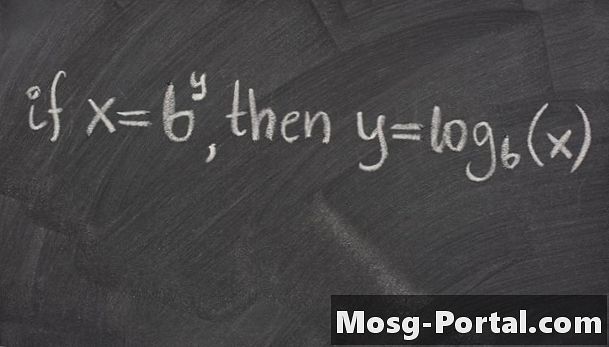
Obsah
Logaritmus je matematická funkcia úzko spojená s exponenciálmi. Logaritmus je v skutočnosti inverziou exponenciálnej funkcie. Všeobecný tvar je log_b (x), ktorý znie „log base b of x“. Často log znamená, že log bez základne obsahuje log 10 log_10 a ln označuje „prírodný log“ log_e, kde e je dôležité transcendentálne číslo. , e = 2,718282 .... Vo všeobecnosti, na výpočet log_b (x) by ste použili kalkulačku, ale znalosť vlastností logaritmov môže pomôcť pri riešení konkrétnych problémov.
vlastnosti
Definícia logaritmickej bázy je log_b (b) = 1. Definícia logaritmickej funkcie je, ak y = b ^ x, potom log_b (y) = x. Niektoré ďalšie dôležité vlastnosti sú log_b (xy) = log_b (x) + log_b (y), log_b (x / y) = log_b (x) - log_b (y) a log_b (x ^ y) = ylog_b (x). Tieto vlastnosti môžete použiť na výpočet logaritmov v rôznych situáciách.
Rýchle triky
Niekedy môžete rýchlo vypočítať log_b (x), ak môžete vyriešiť problém b ^ y = x. Log_10 (1 000) = 3, pretože 10 ^ 3 = 1 000. Log_4 (16) = 2, pretože 4 ^ 2 = 16. Log_25 (5) = 0,5, pretože 25 ^ (1/2) = 5. Log_16 (1/2) = -1/4, pretože 16 ^ (- 1/4) = 1/2 alebo (1/2) ^ 4 = 1/16. Použitím vzorca log_b (xy) log_2 (72) = log_2 (8 * 9) = log_2 (8) + log_2 (9) = 3 + log_2 (9). Ak odhadneme log_2 (9) ~ log_2 (8) = 3, potom log_2 (72) ~ 6. Skutočná hodnota je 6.2.
Zmena základne
Predpokladajme, že poznáte log_b (x), ale chcete vedieť log_a (x). Toto sa nazýva meniace sa základne. Pretože ^ (log_a (x)) = x, môžete napísať log_b (x) = log_b. Ak použijete log_b (x ^ y) = ylog_b (x), môžete to zmeniť na log_b (x) = log_a (x) log_b (a). Rozdelením oboch strán log_b (a) môžete pre log_a (x) vyriešiť: log_a (x) = log_b (x) / log_b (a). Ak máte kalkulačku, ktorá vykonáva 10 protokolov, ale chcete vedieť log_16 (7.3), nájdete ju pomocou log_16 (7.3) = log_10 (7.3) / log_10 (16) = 0,717.